EfficientML Notes
personal notes from the lectures by Prof. Song Han on Efficent ML
Basics of Neural Networks
Link to the original slides.
Neural Network Layers
Fully Connected Layer
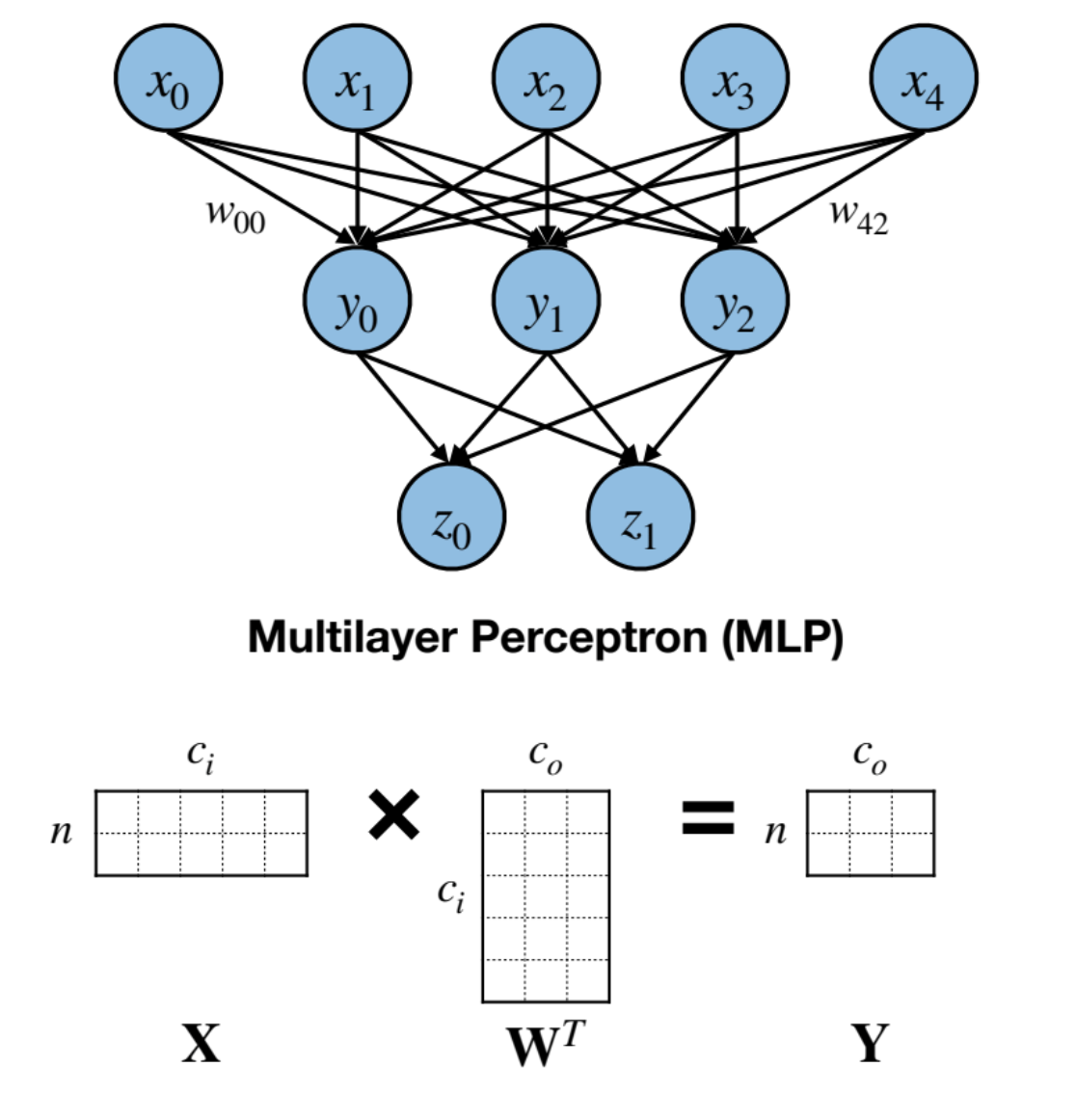
Every neuron in the output layer is connected to every other neuron in the previous layer, resulting in a dense weight matrix.
Input Features: $\mathbf{X} = (n, c_i)$
Weight Matrix: $\mathbf{W} = (c_o, c_i)$
Output Features: $\mathbf{Y} = (n, c_o)$
Bias: $\mathbf{b} = (c_o)$
where, $c_i$ = number of input channels, $c_o$ = number of output channels, and n = batch_size
Convolutional Layer
Output neuron is connected to the input receptive field. Receptive field is usually the kernel shape. Based on the shape of the kernels, we have 1D and 2D convolution operations.
1D Convolutions
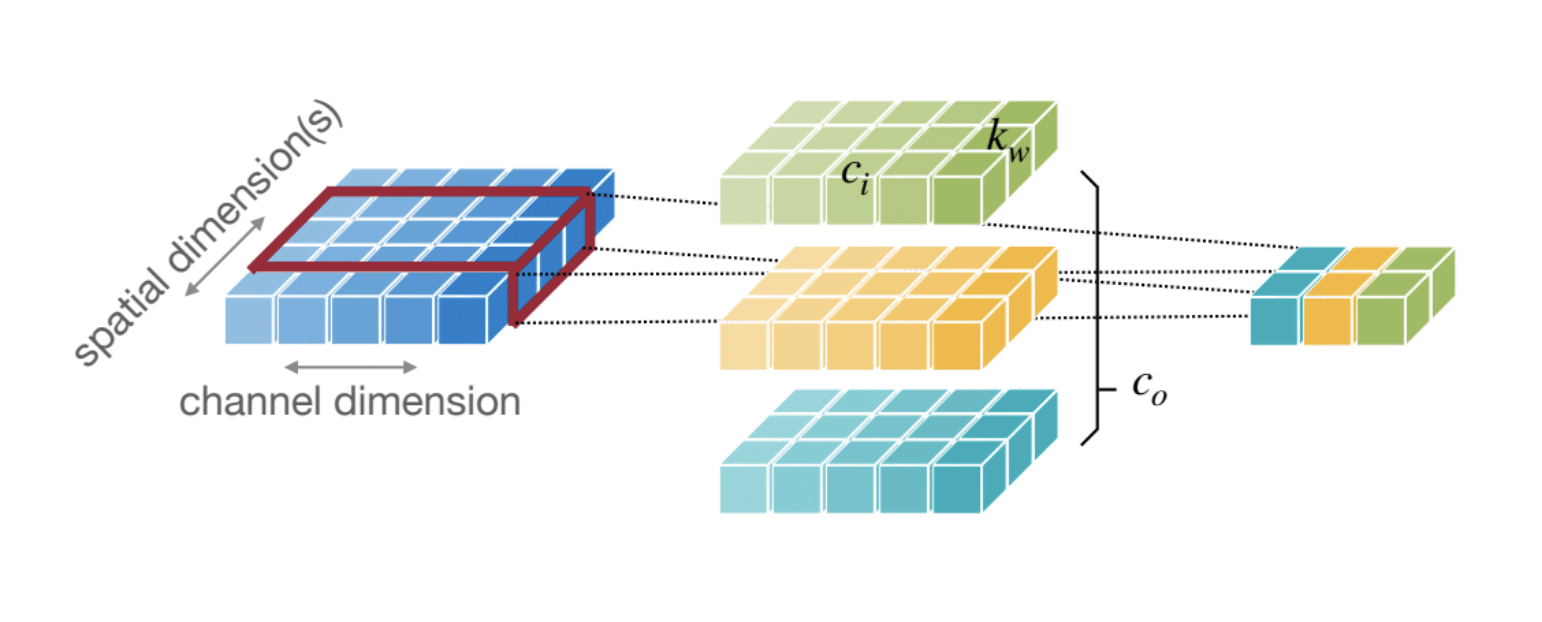
Simpler to visualize from a 2D Kernel, basically you need to match the number of channels and discard either the height or width component.
Input Features, $\mathbf{X} = (n, c_i, w_i)$
Weight Matrix, $\mathbf{W} = (c_o, c_i, k_w)$
Output Features, $\mathbf{Y} = (n, c_o, w_o)$
Bias, $\mathbf{b} = (c_o)$
where, $c_i$ = number of input channels, $c_o$ = number of output channels, n = batch_size and $k_w$ is width of kernel.